A more correct implementation is to notice that this is analogous to taking two planes centered at the origin, and rotating them n time in discrete angular intervals, thus chopping space into uniform areas, resulting in far less distortion.
Neither approach is perfect because you cannot comb a hairy sphere smooth. But the Cube Sphere is far superior, and easier to generate using a difference equation.
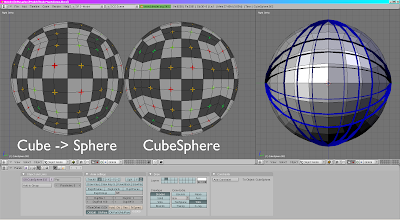
Cube Spheres are good for working with planets and large scale data, but don't have many other uses besides easier texturing of spheres.
..I can;t seem to figure out how to post data to blogger... how to post a .py script?
It's not 100% perfect; copy paste into notepad or something
Here goes nothin':
#!BPY
"""
Name: 'CubeSphere'
Blender: 249
Group: 'AddMesh'
Tooltip: 'Creates a Cube Map sphere'
"""
__author__ = "Izcalli64"
__url__ = ("blender", "http://imaginaryz.blogspot.com");
__version__ = "0.0 2009-11-05"
import Blender
import math;
def generate_grid( ndiv, spanning ):
#
#Optimal spanning value: Unknown
#Optimal spanning equation: Unknown
#
radius = 1.0; #Fixed; don't vary this.
points = [];
ndiv = int( ndiv );
#From experiment; It looks like you need a transformation from radial space to manhatten space:
#
#the only fixed points are the 4 corner points, from which there are lateral and vertical lines;
#These lines must have points distributed on them evenly, by angle.
#These lines are NOT consistent, but do consist of great circle arcs.
#
#SOLUTION:
#
#Generate a cube sphere by taking 2 lists of evenly distributed angles;
#Generate the great circle planes (planes) that intersect the angles;
#Calculate all points on the grid that are the intersections of both:
# The sphere of radius R
# Great circles A and B (will always form a line, no matter what.
#The result:
# Quite a substantial amount less error than the other method. (see .blend)
#The problem:
# Hard to optimize
#
dtr = math.pi/180.0;
mina = 45.0 * dtr; #Minimum angle (45 = pi/4)
maxa = 135.0 * dtr; #Maximum angle (135 = 3*pi/4)
rangea = maxa - mina;
dela = (maxa - mina)/float(ndiv-1);
spanrange = dela * spanning;
#Generate strip angles (for consistency)
stripa = [];
stripa.append( [ mina, math.sin(mina), math.cos(mina) ] );
idex = 1;
ia = mina + dela;
while( idex < (ndiv-1) ):
#Default angles (angular evenness)
#stripa.append( [ ia, math.sin(ia), math.cos(ia) ] );
#Corrected angles:
delv = 2.0 * ((float(idex)/float(ndiv-1)) - 0.5); #-1.0..1.0 range
dels = 0;
if( delv < 0 ):
dels = -1.0;
elif( delv > 0 ):
dels = 1.0;
#Correction quadratic equation (B-spline could be more effective)
#ian = dels * (delv*delv) * spanrange + ia;
#ian = -dels * (1.0 - (delv*delv)) * spanrange + ia;
ian = -dels * (1.0 - abs(delv)) * spanrange + ia;#Very simple; linear. Problem is not linear.
#print delv, dels, -dels * (1.0 - (delv*delv));
stripa.append( [ ian, math.sin(ian), math.cos(ian) ] );
ia += dela;
idex += 1;
stripa.append( [ maxa, math.sin(maxa), math.cos(maxa) ] );
for ex in stripa:
print ex;
#Generate strips:
iy = 0;
while( iy < ndiv ):
ix = 0;
while( ix < ndiv ):
#Plane X / Circle X
PXx = stripa[ix][2]; #cos(x)
PXy = stripa[ix][1]; #sin(x)
PXz = 0;
#Plane Y / Circle Y
PYx = stripa[iy][2]; #cos(y)
PYy = 0;
PYz = stripa[iy][1]; #sin(y)
#Cross product (direction vector to use; can be optimized:)
#nx = PXy * PYz - PXz * PYy;
#ny = PXz * PYx - PXx * PYz;
#nz = PXx * PYy - PXy * PYx;
nx = PXy * PYz;
ny = - PXx * PYz; #Optimized cross product from zero factors
nz = - PXy * PYx;
#Normalize direction vector
nm = math.sqrt( nx*nx + ny*ny + nz*nz );
nx /= nm;
ny /= nm;
nz /= nm;
#Apply scaling of shape
tx = radius * nx;
ty = radius * ny;
tz = radius * nz;
points.append( [tx,ty,tz] );
ix += 1;
iy += 1;
return points;
def generate_points_swizzle( points, comp0, comp1, comp2, neg0, neg1, neg2 ):
newpoints = [];
sw0 = comp0;
sw1 = comp1;
sw2 = comp2;
for P in points:
np = [0,0,0];#[ P[sw0], P[sw1], P[sw2] ];
if( neg0 != 0 ):
np[0] = -P[sw0];
else:
np[0] = P[sw0];
if( neg1 != 0 ):
np[1] = -P[sw1];
else:
np[1] = P[sw1];
if( neg2 != 0 ):
np[2] = -P[sw2];
else:
np[2] = P[sw2];
newpoints.append( np );
return newpoints;
def generate_grid_uv( xdiv, ydiv ):
uvs = [];
iy = 0;
while( iy < (ydiv) ):
ix = 0;
while( ix < (xdiv) ):
u0 = float( ix ) / float(xdiv-1);
v0 = float( iy ) / float(ydiv-1);
uvs.append( [u0,v0] );
ix += 1;
iy += 1;
return uvs;
def generate_grid_facelist( xdiv, ydiv, offset_index ):
faces = [];
iy = 0;
while( iy < (ydiv-1) ):
ix = 0;
while( ix < (xdiv-1) ):
fxy00 = int(offset_index + ix + (iy * xdiv));
fxy10 = int(offset_index + ix + 1 + (iy * xdiv));
fxy01 = int(offset_index + ix + ((iy + 1) * xdiv));
fxy11 = int(offset_index + ix + 1 + ((iy + 1) * xdiv));
faces.append( [fxy00,fxy10,fxy11,fxy01] );
ix += 1;
iy += 1;
return faces;
def generate_cubesphere( in_radius, in_divisions, in_evenness ):
#Generate each cube face, simply rotate it's data to match what we want.
ndiv = in_divisions + 2;
faces = [];
points = [];
uvs = [];
origpoints = generate_grid( ndiv, in_evenness );#x,y,z
faces.extend( generate_grid_facelist( ndiv, ndiv, 0 ) );
points.extend( origpoints );
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
faces.extend( generate_grid_facelist( ndiv, ndiv, len(points) ) );
points.extend( generate_points_swizzle( origpoints, 2,1,0, 0,0,0 ) ); #x,y,z => z,y,x
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
faces.extend( generate_grid_facelist( ndiv, ndiv, len(points) ) );
points.extend( generate_points_swizzle( origpoints, 2,0,1, 0,0,0 ) ); #x,y,z => x,z,y
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
faces.extend( generate_grid_facelist( ndiv, ndiv, len(points) ) );
points.extend( generate_points_swizzle( origpoints, 0,1,2, 1,1,1 ) ); #x,y,z => -x,-y,-z
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
faces.extend( generate_grid_facelist( ndiv, ndiv, len(points) ) );
points.extend( generate_points_swizzle( origpoints, 2,1,0, 1,1,1 ) ); #x,y,z => -z,-y,-x
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
faces.extend( generate_grid_facelist( ndiv, ndiv, len(points) ) );
points.extend( generate_points_swizzle( origpoints, 2,0,1, 1,1,1 ) ); #x,y,z => -x,-z,-y
uvs.extend( generate_grid_uv( ndiv, ndiv ) );
#Scale all points by radius value (lol?)
return points,uvs,faces;
def main():
Draw = Blender.Draw
PREF_RADIUS = Draw.Create(1.0) #"Radius" of cube-sphere
PREF_DIVISIONS = Draw.Create(7) #Divisions per face
PREF_EVENNESS = Draw.Create(0.0) #Evenness of point distribution (by area weighting, so uv texture distortion is absolute minimal at default value)
if not Draw.PupBlock('Add CubeSphere', [\
('Radius:', PREF_RADIUS, 0.01, 100.0, 'Radius for the main ring of the torus'),\
('Divisions:', PREF_DIVISIONS, 0, 256, 'Number of subdivisions to generate'),\
('Evenness:', PREF_EVENNESS, -1.0, 1.0, 'Evenness scaling for evaluation'),\
]):
return;
verts, uvs, faces = generate_cubesphere( PREF_RADIUS.val, PREF_DIVISIONS.val, PREF_EVENNESS.val );
#Every vertex has an exact and corresponding uv value to it (sticky uv)
#As a result, it shall be simple to assign face UV's.
meshobj = Blender.Object.New( 'Mesh', 'CubeSphere' );
meshdata = Blender.Mesh.New();
meshdata.verts.extend(verts);
meshdata.faces.extend(faces);
#Apply uv coordinates:
meshdata.addUVLayer("CubeMap");
meshdata.activeUVLayer = "CubeMap";
if( meshdata.faceUV ):
for f in meshdata.faces:
vinds = [];
for v in f.verts:
vinds.append( v.index );
vdin = 0;
for vdex in f.uv:
uvd = uvs[ vinds[ vdin ] ];
vdex[0] = uvd[0];
vdex[1] = uvd[1];
vdin += 1;
else:
print "#ERROR; Face UV could not be enabled??";
meshdata.calcNormals();
meshdata.update();
meshobj.link( meshdata );
Blender.Scene.GetCurrent().objects.link( meshobj ); #Is this deprecated? #ERROR
main();
#Blender.Draw.PupMenu("Error%t|This script requires a full python installation")
No comments:
Post a Comment